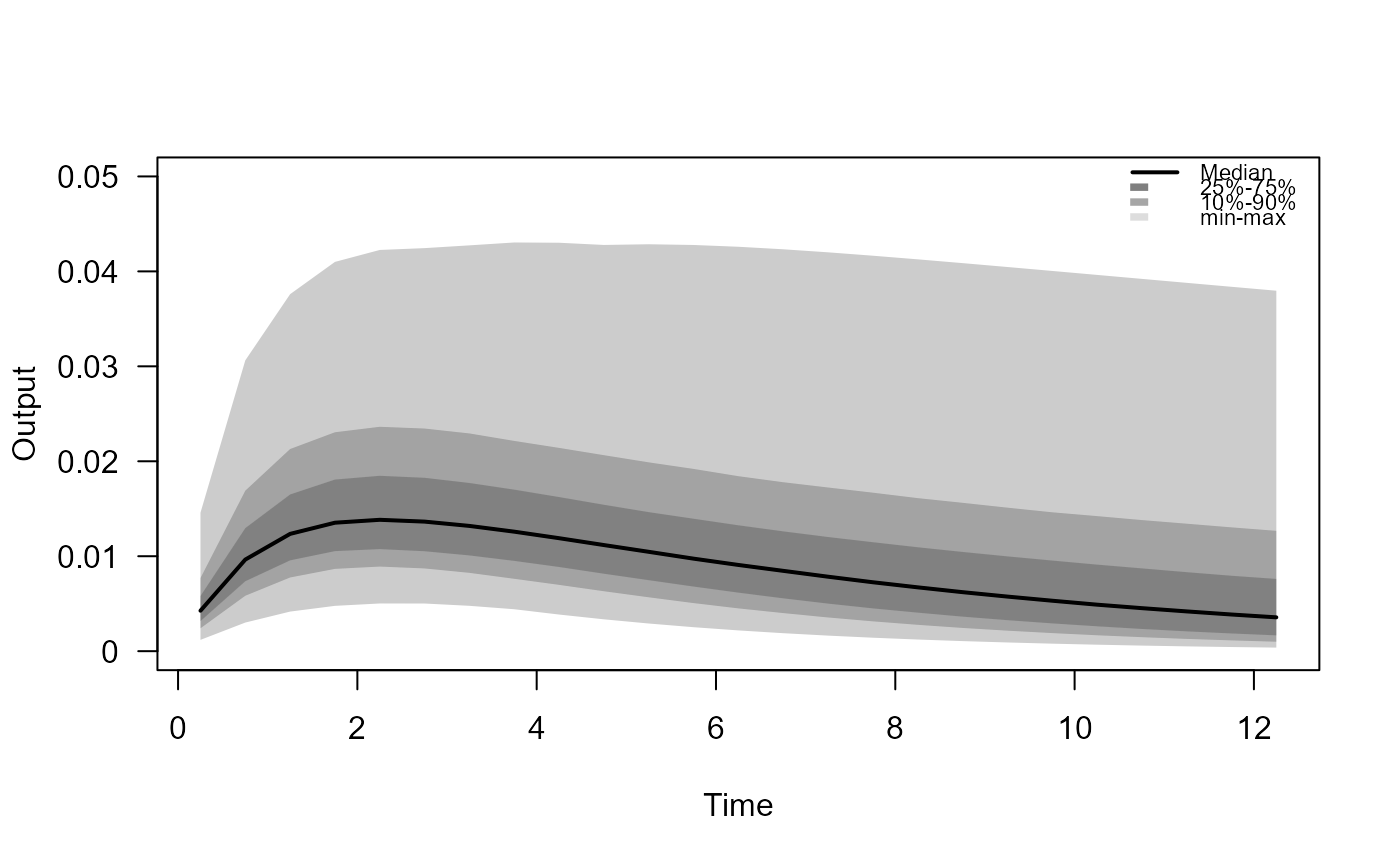Solve PK Model Through deSolve Package or Analytical Function

Solve time-dependent quantities/concentrations of different variables in PK model through the imported ode function in deSolve package. It can also be used to solve the function with analytical solution.

Usage

solve_fun(
  x,
  time = NULL,
  initParmsfun = "initParms",
  initState,
  dllname = NULL,
  func = "derivs",
  initfunc = "initmod",
  outnames,
  method = "lsode",
  rtol = 1e-08,
  atol = 1e-12,
  model = NULL,
  lnparam = F,
  vars = NULL,
  tell = T,
  ...
)

Arguments

x

a list of storing information in the defined sensitivity function.

time

a vector to define the given time sequence.

initParmsfun

a character for the given specific initial parameter function.

initState

a vector that define the initial values of state variables for the ODE system.

dllname

a string giving the name of the shared library (without extension) that contains the compiled function.

func

the name of the function in the dynamically loaded shared library.

initfunc

the name of the initialization function (which initialises values of parameters), as provided in dllname.

outnames

the names of output variables calculated in the compiled function func.

method

method used by integrator (deSolve).

rtol

argument passed to integrator (deSolve).

atol

argument passed to integrator (deSolve).

model

the defined analytical equation with functional output.

lnparam

a logical value that make the statement of the log-transformed parameter (default FALSE).

vars

a character for the selected output.

tell

a logical value to automatically combine the result y to decoupling simulation x.

...

additional arguments for deSolve::ode method.

References

Soetaert, K. E., Petzoldt, T., & Setzer, R. W. (2010). Solving differential equations in R: package deSolve. Journal of Statistical Software, 33(9), 1–25.

See also

pksim

Examples

  q <- "qunif"
  q.arg <- list(list(min = 0.6, max = 1.0),
   list(min = 0.5, max = 1.5),
   list(min = 0.02, max = 0.3),
   list(min = 20, max = 60))

  params <- c("F","KA","KE","V")

  set.seed(1234)
  x <- rfast99(params = params, n = 200, q = q, q.arg = q.arg, rep = 20)

  time <- seq(from = 0.25, to = 12.25, by = 0.5)
  y <- solve_fun(x, model = FFPK, time = time, vars = "output")
#> Starting time: 2024-11-27 17:35:04.35705
#> Ending time: 2024-11-27 17:35:04.646113

  pksim(y) # Visualize uncertainty of model output